FRANÇAIS

2007 Spring School
Viability: Models, Algorithms and Applications in Finance and Environmental-Economics
April 16-20, 2007
Registration  Speakers  Venue  Schedule  Links   Accommodation   Contact   Poster   Online information Organised by: Michèle Breton, CREF, GERAD, HEC Montréal Georges Zaccour, Chair in game theory and management, GERAD, HEC Montréal Sponsors: Centre for Research on e-finance (CREF) Chair in game theory and management Group for Research in Decision Analysis (GERAD)

Introduction

The aim of this tutorial is to explain how the mathematical and algorithmic tools of viability theory can be used to solve some issues in both mathematical finance and environmental studies. In a nutshell, viability theory investigates evolutions

• in continuous time, discrete time, or an "hybrid" of the two when impulses are involved,

• constrained to adapt to an environment,

• evolving under contingent, stochastic or tychastic uncertainty,

• using for this purpose controls, regulons (regulation controls), subsets of regulons, and in the case of networks, connectionist matrices,

• regulated by feedback laws (static or dynamic) that are then "computed" according to given principles, such as the inertia principle, intertemporal optimization, etc.,

• co-evolving with their environment (mutational and morphological viability),

• and corrected by introducing adequate controls (viability multipliers) when viability or capturability is at stakes.

  ---

Topics Covered

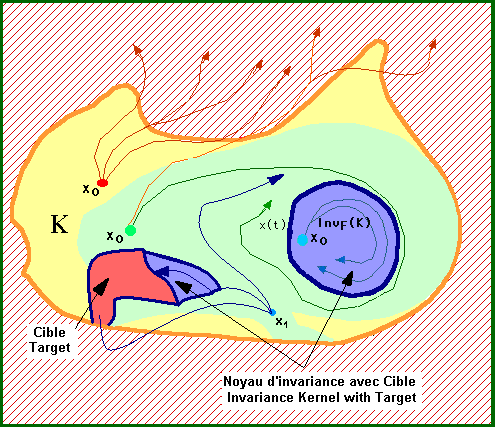
1. Main concepts and examples: Viability Kernels of an environment and Capture Basins of a target viable in an environment. Viable Feedbacks. Examples. Viability Algorithms (principle). Cascade of environments. Chaining of feedbacks and concatenation of environments. Tychastic uncertainty. Comparison between stochastic and tychastic viability kernels

2. Environmental Applications: Inertia Function, dynamic of renewable resources, fisheries, heavy and cyclic evolutions, control of Green House Gases,

3. Mathematical finance: Viability formulation of the pricing and management of portfolios and cash flows, applications to options, implicit volatility

4. New perspectives: viability multipliers, impulse systems and mutational equations

5. Back to mathematics: Viability and Invariance Theorems, Hamilton-Jacobi equations and other issues.

Lecture notes and executables of software will be provided and flexibility is planned to answer questions of interest by the participants (closed-loop pedagogy).