Research interests

Blackbox Optimization

Several engineering optimization problems do not possess the necessary structure to be approached by traditional optimization methods. Indeed, the functions and constraints defining the problem are often given in the form of a blackbox (usually evaluated by a computer code). These black boxes can be costly, inaccurate, can fail for reasons internal to the box, and useful derivatives are unavailable. An important part of my research focuses on the development, analysis and the application of mesh adaptive direct search methods.

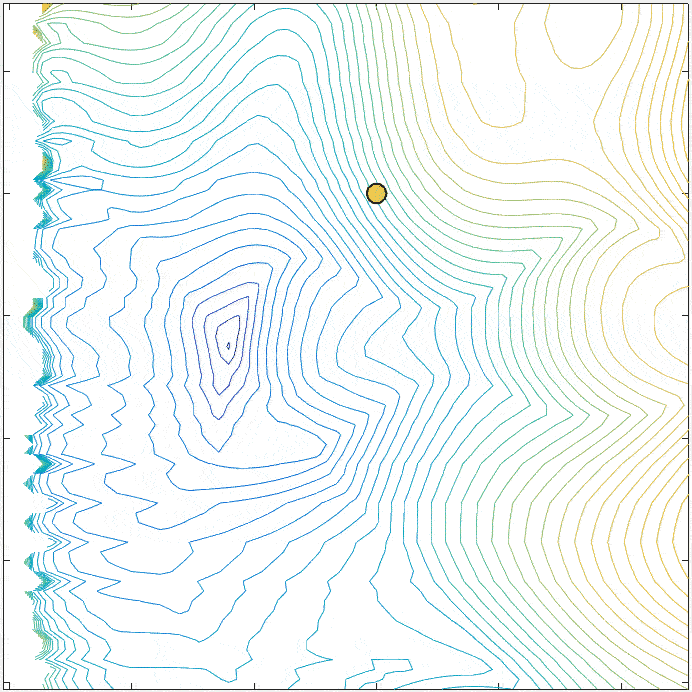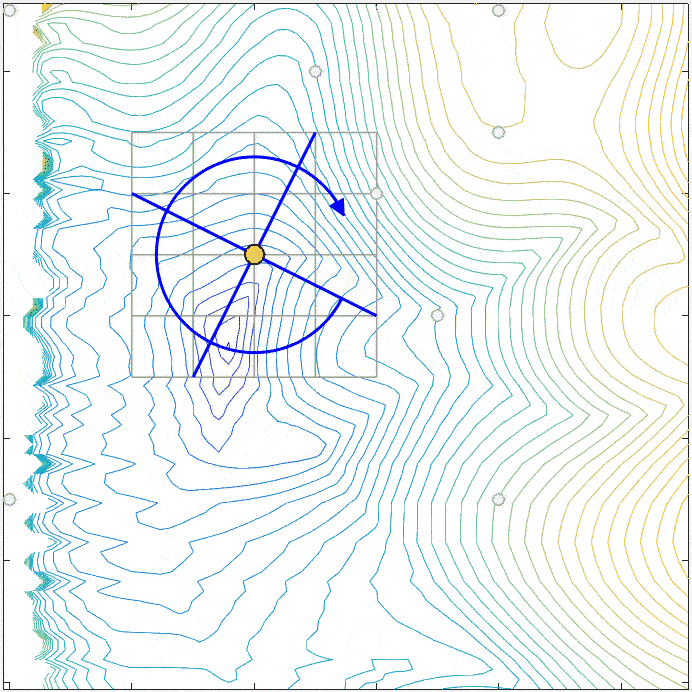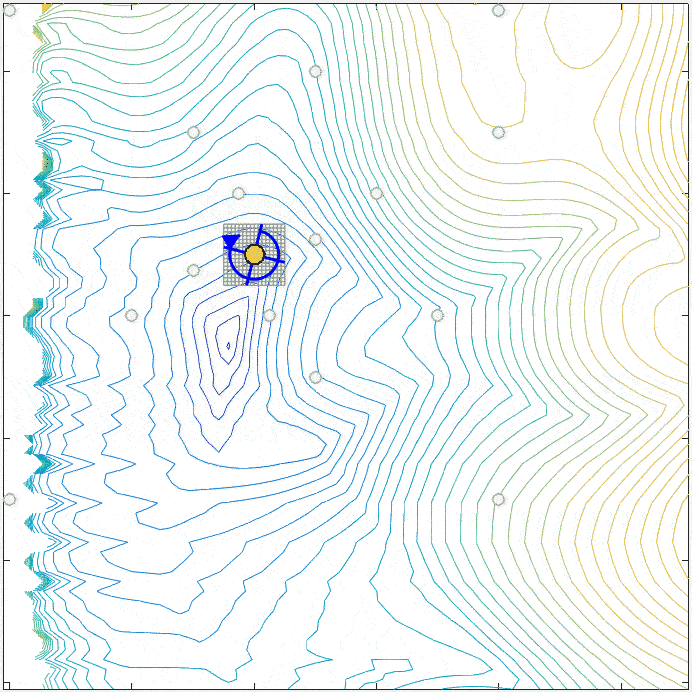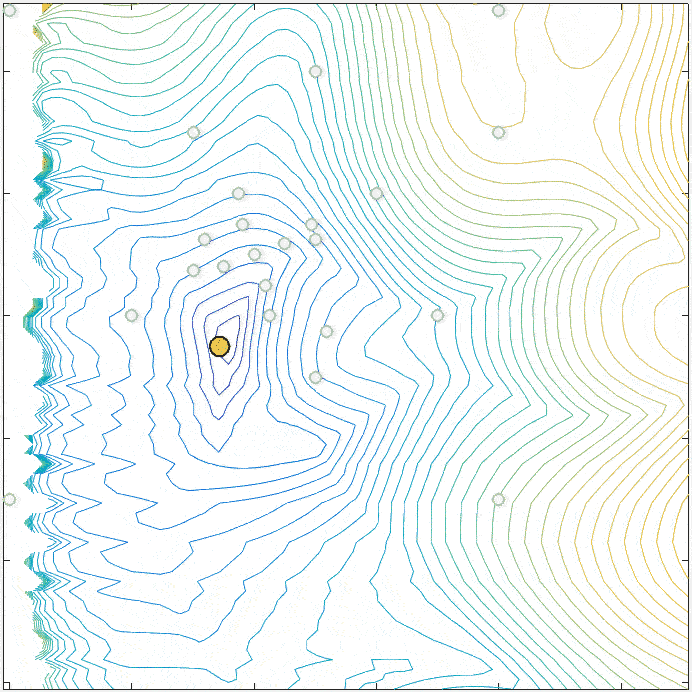
The figure on the right illustrates a series of poll steps of the Mesh Adaptive Direct Search algorithm. I talk about blackbox optimization in the video below.

Global Optimization

A second part of my research involves exact methods of global optimization for classes of problems whose structure is well defined and known, but not convex, such as bilevel, quadratic, bilinear or integer programming. The structure of these problems is identified and exploited in order to develop efficient algorithms. We apply these techniques to problems of planar geometry.